IEEE 754 Single and Double Precision Formats Explained

Introduction

Assuming that you already know how signed and unsigned integers are represented in memory (two’s complement format), we’re now going to explore another format which is used to represent real numbers.

Converting floating point numbers to binary

First of all let’s start with simple examples. How would you convert 35.25 to binary? We can do it by two simple steps: convert the integer part to binary; then convert fractional part to binary. Since we know how to convert 35 to binary (100011) let’s see how to convert 0.25 to its binary representation.
In order to do this we need to multiply the fractional number by 2 and write down integer part of the result until we get 0 in the fractional part:

0.25 x 2 = 0.50 // integer part is 0
0.50 x 2 = 1.0 // integer part is 1, we stop here since fractional part is 0

So, 0.25 is 01 in binary and 32.25₁₀ = 100011.01₂. You can observe that if the fractional part can eventually be brought to 0 by multiplying with 2 then it can be represented very precise in memory, otherwise it will be bunch of repeting 1s or 0s. To see an example, let’s convert 0.3 to binary:

0.3 x 2 = 0.6 // integer part is 0
0.6 x 2 = 1.2 // integer part is 1, then we take 0.2 as fractional part
0.2 x 2 = 0.4 // integer part is 0
0.4 x 2 = 0.8 // integer part is 0
0.8 x 2 = 1.6 // integer part is 1, then we take 0.6 as fractional part
0.6 x 2 = 1.2 // integer part is 1, then we take 0.2 as fractional part
...
// goes to infinity

You can already see that we again got to multiply 0.6 by 2 and this case is going to appear many many times. That’s why 0.3 cannot be represented in binary very precise. So, 0.3₁₀ = 0.01001100110011001101₂.

IEEE 754 32 bit single precistion format

In decimal we can represent floating point numbers in different formats. For example, 4539.4 can also be written as 4.5394 x 10³ or 45394 x 10^-1. For standardizing the representation of real numbers in binary, the committee created a standard format which is called IEEE 754. They said that, when converting to binary, keep only one digit to the left of the radix point (they call is normalized form). For example:

37.25₁₀ = 100101.01₂ = 1.0010101 x 2⁵
7.625₁₀ = 111.101₂ = 1.11101 x 2²
0.3125₁₀ = 0.0101₂ = 1.01 x 2^-2

Since the number before radix point is always 1, we don’t need to store it. We just need to store mantissa (number after decimal point) and the biased exponent (power of 2). Here is whay IEEE 754 single precision format looks like:

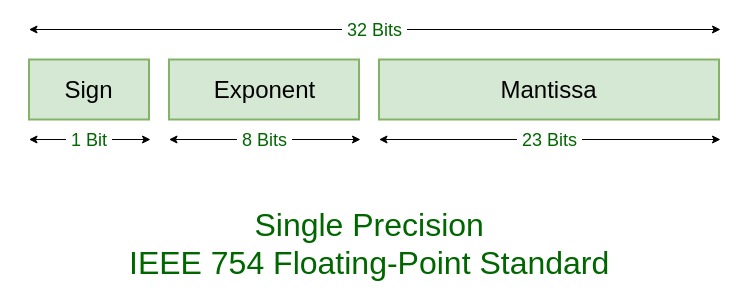
As you see IEEE single precision format is just 32 bit field which uses 1 bit to store sign (0 for positive numbers, 1 for negative), 8 bits for biased exponent (exponent + 127) and the rest of 23 bits for mantissa. Let’s peek a number from above and convert it to IEEE 754 single precision format.

37.25₁₀ = 100101.01₂ = 1.0010101 x 2⁵

To convert it to IEEE 754 single precision format:

• we set first bit to 0,
• then we store 0010101 in mantissa part,
• then we store 132 (127 + 5) and store it in exponent part (127 is a special number called bias)

So, 37.25 is 01000010 00010101 00000000 00000000 in IEEE 754 single precision format. You can use this website to play with any number you want.

IEEE 754 64 bit double precision format

If you understood how to convert to IEEE 754 single precision format then it is simple. Double precision format can hold up to 64 bits (therefore it’s more precise) while single precision format can store only 32 bits. Here is the image:

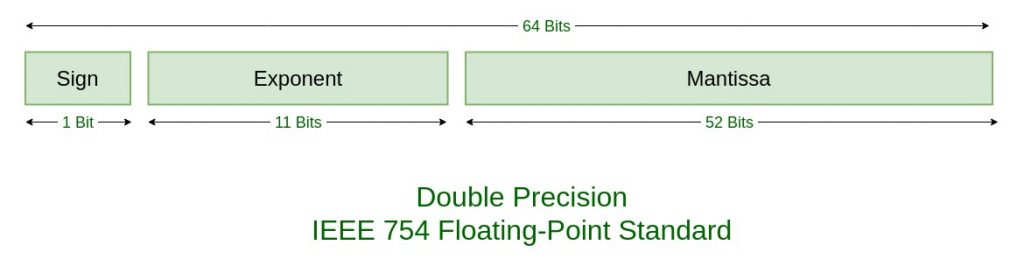
I believe it’s clear and you can do also convert from IEEE 754 to floating point number now 😉 (otherwise check this video)

Ok, so what’s that bias?

The number that you saw above - 127 - is called bias and used to simplify comparison of numbers in IEEE 754 format.
I am not going to go into much detail but try to convert 0.9 and 1.1 to IEEE 754 32-bit format and then try to compare them in that format. With biased exponent you can compare two numbers by just comparing their biased exponents otherwise you have to convert numbers back to decimal format and then compare them.

Special cases

IEEE 754 format contains some special cases for representing some numbers such as Infinity, NaN etc. Here are those case:

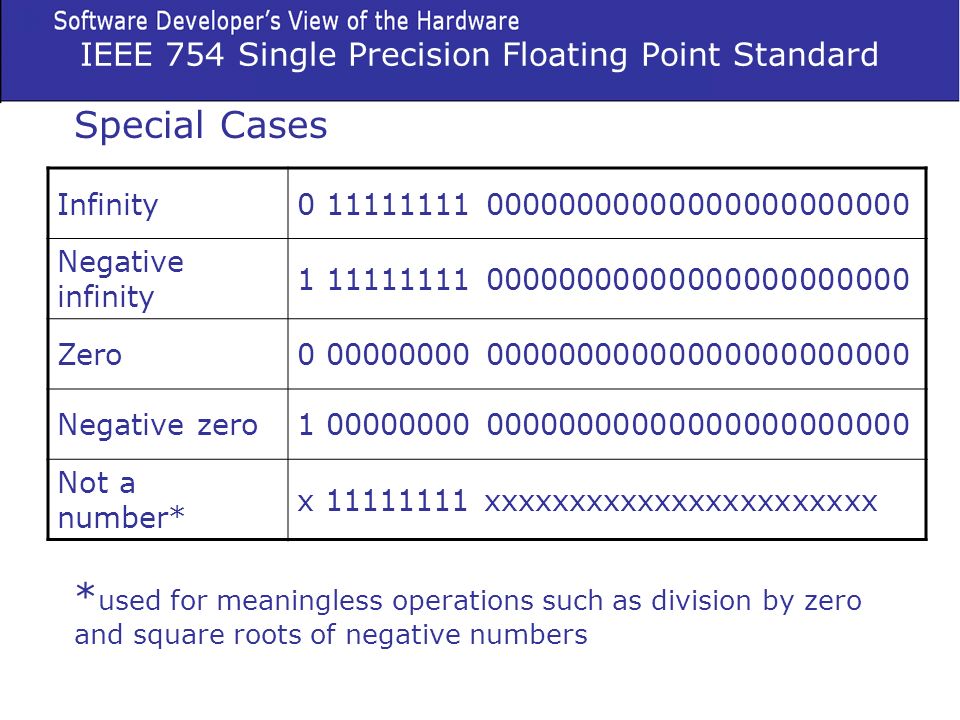
If you’re a JavaScript developer and always wondered why there’re two zeroes in JavaScript, here is the answer: ECMAScript specifications require JavaScript engines to store all numbers in IEEE 754 duble precision format.

Conclusion

Thanks for reading!

If you find any mistakes in any of my articles, please do not hesitate to fix them and send me a PR.

https://github.com/orkhan-huseyn/my-blog